Here’s a no-brainer tip for you: space vectors are useful when designing electric motors. Duh.
However, there’s one specific detail you might not know: they are also extremely handy when computing the back-EMF waveform, or induced no-load voltages.
Specifically, they can reduce the number of samples – or time-steps, or rotor positions – needed to obtain a good estimate of the waveforms. This can save time in optimization or pre-design, or help deal with incomplete data that you may have been dealt with.
Here’s how it goes:
Naiive back-EMF computation
Normally, back-EMF calculation has only two steps:
- You get your phase flux linkages
from your finite element software. - You numerically differentiate them with
.
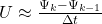Space-vector based approach
By contrast, here’s how it works with space vectors:
- You have your phase flux linkages.
- You transform them to the rotating reference frame.
- You do the numerical differentiation in the rotating frame.
- You transform the results back to phase quantities if needed.
Here, only step number 3 needs some extra caution. Remember that the synchronous-frame components are computed with
,
where 
is a rotation matrix and 
is the well-known Park-Clarke matrix.
Now, note that both the rotation matrix and the synchronous-frame fluxes are generally time-dependent, so the differentiation results, after some simplifications and notation-abusing, in two components:
Why it’s smart
Now, why do I claim (without much proof, mind you) that this approach is better than using the allegedly-naiive direct approach?
Well, if our polyphase system is good – close-ish to sinusoidal and reasonably balanced – then the synchronous components 
are roughly constant.
Which, in turn, means that our voltage is largely determined by the 
term, and only a small part depends on the ripple term 
. As numerical differentiation amplifies any numerical errors – such as those stemming from a low number of samples – one can argue this is more accurate than direct differentiation.
Why it’s smart, Part 2
Of course, this approach is not smart for any arbitrary signal. Instead, it’s only smart for actual, reasonably well-behaved polyphase systems.
After all, for the dq-components to be roughly constant, the system has to be roughly balanced: roughly sinusoidal phase quantities with roughly the same amplitudes and roughly the lag between phases.
The space-vector approach sort of encodes this apriori information into the differentiation.
And mind you, it seems to work better the more phases we have. After all, the dq-transformation can be generalized into arbitrary phase counts (see a fantastic paper here). We just get more synchronous components, corresponding to the first, third, fifth harmonic and so on, and additionally a mean or zero-sequence components. The transformation is lossless when you include all the components, mind you, allowing perfect reconstruction of the original signals.
Demonstration
As an example, I computed the back-EMFs of a six-phase outrunner PM motor with EMDtool.
Link to analysis script file here.
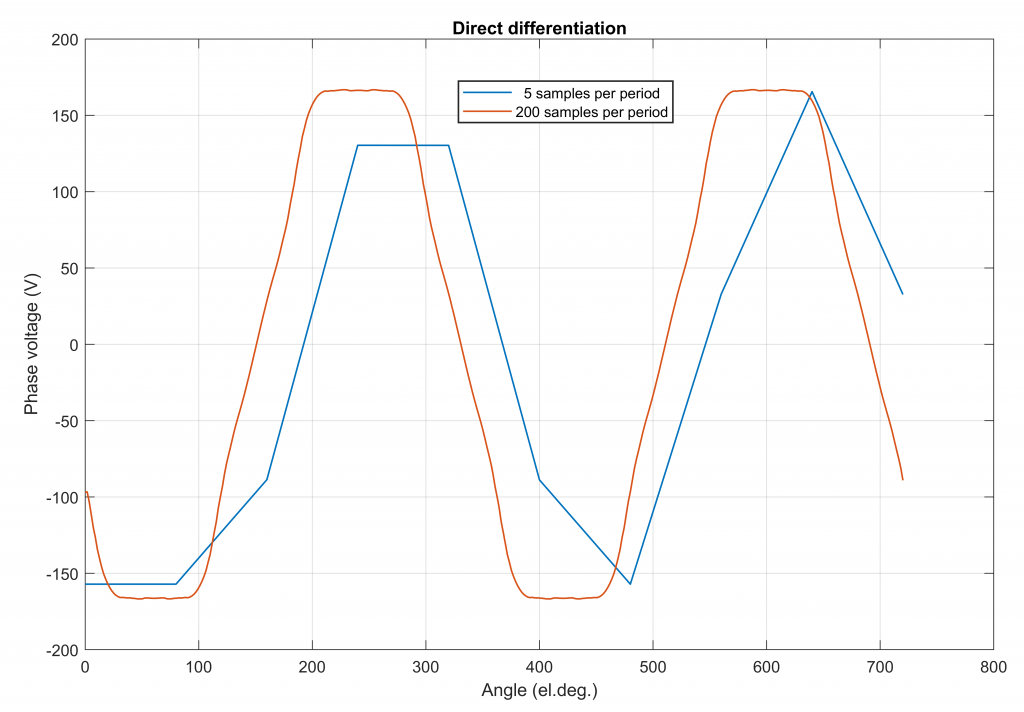
To really demonstrate the point, I calculated the voltage waveforms using a pathetic 5 steps per electrical period, and a good 200 steps.
To demonstrate the ‘information-utilizing’ feature of the space-vector approach I then linearly interpolated the results into 1000 steps per period. This interpolation was done in the static frame for the naiive approach, and in the synchronous frame for the proposed smart-person approach.
Below, you can find the results. As you can see, the direct differentiation approach is pretty much useless with 5 steps – as expected. By contrast, the space-vector method yields quite a good results even with such coarse sampling – reflecting the typically-good BEMF waveforms of concentrated windings.
Check out EMDtool - Electric Motor Design toolbox for Matlab.
Need help with electric motor design or design software? Let's get in touch - satisfaction guaranteed!
